Quantum Virtual Link Generation via Reinforcement Learning

Abstract

• Quantum networks leverage quantum entanglement as a fundamental building block.
• When two qubits are entangled, their states exhibit non-classical correlations, enabling novel applications such as quantum key distribution and distributed quantum computing, which are not possible with classical communication.
• However, quantum entanglement is a probabilistic process heavily dependent on the characteristics of the involved devices, such as optical fibers, lasers, and quantum memories.
• Managing this process to maintain entanglement with high quality for as long as possible is a stochastic control problem.
• This process can be modeled as a MDP and solved using the RL framework.
• In this work, we employ RL to develop an entanglement management policy that surpasses the current State-of-the-Art policies, particularly in scenarios where precise models of the quantum devices are unavailable.
• Reference: (Aparicio-Pardo et al., 2023)

---

Introduction

1. 양자 인터넷의 등장

• 최근 양자 물리학 원리(quantum physics principles)가 컴퓨터 네트워크에 적용되며 연구와 산업 분야에서 주목받고 있음
• IETF(Internet Engineering Task Force)가 제안한 양자 인터넷(Quantum Internet)의 표준화 시도가 이를 증명 (Kozlowski et al., 2023), (Wang et al., 2024)
• 양자 얽힘(quantum entanglement)은 양자 통신(Quantum Communication)을 위한 기본 자원
  • 이를 통해 양자 암호 키 분배(quantum key distribution)와 분산 양자 컴퓨팅(distributed quantum computing)과 같은 응용 실현 가능

2. 양자 얽힘의 특성과 문제

• 양자 얽힘은 확률적 과정(probabilistic process)으로, 관련 통신 장치(광섬유(optical fiber), 레이저(laser), 양자 메모리(quantum memory) 등)의 특성에 크게 의존
• 얽힘 관리는 확률 제어 문제(stochastic control problem)로, 마르코프 결정 과정(Markov Decision Process, MDP)**으로 공식화 가능
• 본 연구에서는 두 원격 통신 노드(remote communication nodes) 간의 얽힘을 설정할 때 DRL의 적용 가능성 조사

3. 양자 비트(Qubit)와 얽힘(Entanglement)

• 양자 비트(Qubit)는 고전 비트(classical bit)의 양자적 대응물
  • 고전 비트는 “0” 또는 “1”의 상태만 가지지만, 양자 비트는 두 상태의 중첩(superposition) 상태를 가짐
  • 측정 후 확률에 따라 “0” 또는 “1” 상태로 결정됨
• 얽힘(Entanglement):
  • 두 양자 비트가 얽히면 각 상태를 독립적으로 설명할 수 없음
  • 한 쪽 비트 상태가 변하면, 물리적 거리에 관계없이 다른 비트의 상태도 함께 변화
  • 얽힘은 양자 암호와 분산 양자 컴퓨팅 같은 비고전적(non-classical) 응용의 핵심 요소

4. 양자 네트워크(Quantum Network)

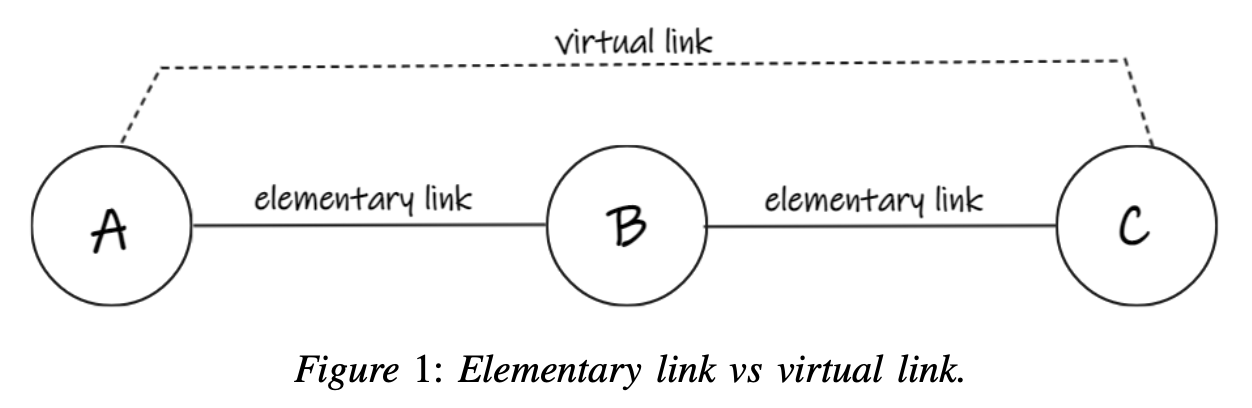
• 양자 네트워크는 얽힘 상태를 분배하고 양자 비트(Qubit)를 교환할 수 있는 노드(node)들로 구성.
  • 노드들은 광섬유(optical fiber) 또는 위성 레이저 링크(satellite laser link)로 연결.
• 얽힘 상태 설정:
  • 두 인접 노드에 위치한 양자 비트 간 얽힘은 기본 링크(elementary link)를 구성.
  • 두 노드 간 얽힘 성공 확률(\(P_{e_{i,j}}\))은 거리 증가에 따라 지수적으로 감소
    • Short-distance entanglements (like A-B, in Fig. 1) are more likely to succeed than long-distance entanglements (like A-C, in Fig. 1)
• 가상 링크(Virtual Link) 생성:
  • 얽힘 교환(Entanglement Swapping)을 통해 두 개의 기본 링크를 결합
    • 예) 기본 링크 A-B와 B-C를 소비하여 A-C라는 장거리 가상 링크 생성
  • 얽힘 교환을 수행하는 중간 노드는 양자 리피터(Quantum Repeater)
  • 양자 리피터는 기본 링크들을 양자 메모리(Quantum Memory)에 저장 후 사용
    • 예) B는 A-B와 B-C의 기본 링크를 양자 메모리에 저장 후 사용

5. 양자 메모리 수명(Quantum Memory Lifetimes)

• 양자 메모리에 저장된 얽힘 상태가 원래 상태를 유지할 확률(메모리 효율(memory efficiency), \(\eta\))은 시간이 지남에 따라 감소
  • 이 과정은 데코히어런스(Decoherence)로 알려짐.
  • 얽힘 교환 성공 확률(\(P_s\))은 가장 오래된 양자 메모리의 메모리 효율 \(\eta\)에 의존

6. 본 연구의 기여

• 양자 가상 링크 생성 과정을 고전적 MDP(Classical MDP)로 모델링하고, DRL 알고리즘을 사용하여 최적의 생성 정책(policy)을 도출
• 본 연구는 기본 링크의 나이(age)를 추적하는 새로운 방법을 제안:
  • 기존 연구에서는 링크 생성 성공 시점의 타임스탬프, 즉 링크의 나이를 고려하지 않음

심볼	설명	비고
\(P_{e_{i,j}}\)	두 노드 간 얽힘 성공 확률
\(\eta\)	양자 메모리 효율	양자 메모리에 저장된 얽힘 상태가 원래 상태를 유지할 확률 (저장 시간에 따라 감소, Mims 모델 따름 (Ortu et al., 2022))
\(P_s\)	얽힘 교환 성공 확률	가장 오래된 양자 메모리의 메모리 효율, 즉, \(\eta\)에 의존
\(t_c\)	컷오프 시간

---

Related Works

1. Quantum Decision Process(QDP)

• Quantum Decision Process(QDP)는 MDP의 양자적 일반화로, Khatri의 박사 논문(Khatri, 2021)에서 제안됨.
• 양자 컴퓨터의 사용을 전제로 하는 QDP의 주요 구성 요소 -양자 상태(Quantum State) - QDP에서는 상태를 양자 상태(Quantum State)로 표현 - 양자 상태는 상태 벡터로 나타나며, 중첩(Superposition)과 얽힘(Entanglement)을 포함할 수 있음
  • 양자 행동(Quantum Action)
    • QDP의 행동은 고전적 액션이 아닌 양자 연산자(Quantum Operator)로 표현됨
    • 이는 유니터리 연산이나 측정과 같은 양자역학적 연산으로 구현되며, 상태에 작용하여 새로운 상태를 생성함
  • 양자 상태 전이
    • 전이 확률이 고전적 확률 분포 대신 양자 연산에 의해 결정됨
    • 양자 연산은 상태를 변환하면서 고전적 시스템과 달리 비선형적이고 중첩된 결과를 생성할 수 있음
  • 보상 함수(Reward Function)
    • QDP의 보상 함수는 양자 상태를 기준으로 정의되며, 특정 양자 상태 또는 결과를 얻는 것에 대한 가치(value)를 표현함
    • 보상 함수는 상태와 행동의 조합에 따라 달라질 수 있음

2. 이 논문의 접근 방식

• 기존 QDP 모델과는 달리, 이 논문은 측정된 물리적 속성으로 기술된 상태와 거시적 수준의 액션으로 구성된 클래식 MDP로 모델링함.
• Khatri의 아이디어 중 현재 기술 수준에서 활용 가능한 것들을 도입, 양자 컴퓨터 개발을 기다릴 필요 없이 구현 가능성을 제시함.

3. 논문 모델링 대상

• 논문의 대상은 Khatri 논문의 부록 D에서 제시된 얽힘 교환(entanglement swapping)을 이용한 가상 링크 생성
• 가상 링크 생성은 다음 두 가지 맥락에서 연구됨:
  • 양자 중계기(Quantum Repeaters) 체인에서의 장거리 얽힘 생성
  • 양자 얽힘 라우팅(Quantum Entanglement Routing)에서의 Mesh 네트워크 기반 얽힘 생성

4. 기존 연구와의 차이점

• 기존 연구는 링크 생성의 히스토리(타임스탬프)를 무시
• 즉, 가상 링크 생성 시 무한 메모리 컷오프 시간 정책(infinity memory cutoff-time policy)을 따름
  • 초기 링크가 성공적으로 얽힌 이후 다음 링크가 성공적으로 얽힐 때까지 초기 링크는 원래 상태를 지속적으로 유지할 확률을 100% 로 설정
  • 오래된 링크의 더 큰 열화(decoherence)가 얽힘 교환 성공 확률(\(P_s\))에 미치는 영향을 고려하지 않음
• 열화(decoherence)
  • 큐비트 상태가 시간이 지남에 따라 점진적으로 손실되는 과정
  • 원인: 양자 메모리가 환경과 상호작용하면서 완벽히 고립될 수 없기 때문

5. 이 논문의 개선점

• 기존 접근법의 단점을 보완하여, 히스토리와 열화(decoherence) 영향을 포함한 MDP 모델링을 제안.

---

Reinforcement Learning for Virtual Link Generation

1. 문제 정의: 가상 링크 생성 문제

• 얽힘 교환을 통해 두 개의 기본 링크로부터 가상 링크를 생성할 때 시간당 성공적인 `얽힘 교환` 횟수(가상 링크 생성률)를 최대화하는 문제
• 얽힘 교환 성공 확률(\(P_s\)):
  • 두 개의 기본 링크가 성공적으로 생성되어야 얽힘 교환 시도 가능
  • 처음 생성된 기본 링크가 오래될수록 성공 확률 감소
• 컷오프 시간(\(t_c\))
  • 얽힘 상태를 유지하다가 폐기하는 시점을 결정하는 시간 임계값
  • 얽힘 품질 관리
    • 얽힘 상태는 시간이 지남에 따라 열화(decoherence) 현상으로 인해 점차 품질이 저하됨
    • 품질이 낮아지면 얽힘 교환의 성공 확률이 감소하므로, 특정 시간 이후 품질 저하된 얽힘 상태를 폐기하는 것이 유리함
  • 리소스 최적화
    • 얽힘 상태를 오래 유지하면 성공 확률은 감소하지만, 새로 생성하지 않으므로 리소스를 절약할 수 있음
    • 반대로, 얽힘 상태를 폐기하고 새로 생성하면 높은 성공 확률을 얻을 수 있지만, 생성 과정에서 비용과 시간이 소모되고 얽힘 교환 시도를 지연시킴
  • 얽힘 폐기와 재생성을 통해 얽힘 교환 성공 확률(\(P_s\))을 높일 수 있음
• 컷오프 시간 설정의 중요성

짧은 컷오프 시간	긴 컷오프 시간
얽힘 상태를 빠르게 폐기하고 새로 생성함	얽힘 상태를 오래 유지하며 새로운 생성 빈도를 줄임
얽힘 교환 성공 확률은 높아질 수 있지만, 새로운 링크 생성의 반복으로 인해 전체 과정이 지연될 가능성이 높아짐	리소스를 절약하며 빠르게 교환 시도를 진행할 수 있지만, 얽힘 교환의 성공 확률은 낮아질 수 있음
리소스 소모 증가	열화(decoherence) 영향이 크다면 교환 실패 가능성이 높아짐

• 컷오프 시간 결정의 어려움
  • 얽힘 생성 성공 확률(\(P_{e_{i,j}}\))와 얽힘 교환 성공 확률(\(P_s\))은 다양한 환경적 요인(예: 광섬유 길이, 양자 메모리 특성)에 따라 변화
  • 최적의 컷오프 시간을 설정하려면 다음을 고려해야 함
    • 얽힘 상태의 품질 변화 속도(열화(decoherence) 영향)
    • 새로운 얽힘 생성의 성공 확률 및 소요 시간
    • 전체 가상 링크 생성률을 극대화하는 시간-성능 균형

2. 양자 얽힘 관리 문제에 대한 MDP 정의

• 타임 스텝(time step) \(t\) :
  • 제어 에이전트는 현재 상태 \(s_t\)를 관찰한 후 특정 행동 \(a_t\)를 적용
  • 이 행동의 실행은 상태 전이 확률 \(p(s_t, a_t, s_{t+1})\)에 의하여 새로운 상태 \(s_{t+1}\)로의 전환을 유발
  • 에이전트는 상태-행동 쌍 \((s_t, a_t)\)의 평가에 따라 보상 \(r_{t+1}\)을 받음
  • 에이전트는 새로운 상태 \(s_{t+1}\)를 관찰하고 이 과정을 반복
• MDP의 경로(trajectory):
  • 초기 상태 \(s_0\)에서 시작하여 다음과 같은 경로를 생성: \(s_0, a_0, r_1, s_1, a_1, r_2, s_2, a_2, r_3, \dots\)
  • 이 경로는 에이전트 정책(policy) \(\pi(s, a)\)에 따라 생성
• 시스템 상태:
  • 두 기본 링크(elementary links)와 가상 링크(virtual link)의 상태(행동)를 연결(concatenate)하여 구성
  • 각 링크의 상태는 벡터 \(s = [x, m]\)로 표현:
    • \(x\): 얽힘(entanglement) 상태
      • \(x = 1\): 얽힘이 활성 상태
      • \(x = 0\): 얽힘이 비활성 상태
    • \(m\): 얽힘의 나이(age)
      • 얽힘이 비활성 상태(즉, \(x = 0\))인 경우 \(m = -1\)
• 각 링크별 가능한 행동:
  • 각 기본 또는 가상 링크에 대해 다음 두 가지 행동 중 하나 선택:
    1. 재설정(reset):
       • 링크 생성 재시도
       • 확률 \(P_{e_{i,j}}\) 및 \(P_s\)에 따라 확률적 전환 유발
       • 해당 링크 상태 \(s\)에 대해
         • \(x\)가 1 또는 0으로 변경
         • \(x=1\)이라면 \(m\)은 0으로 변경
    2. 대기(wait):
       • 링크 생성이 재시도되지 않으며, 현재 링크 상태는 그대로 유지
       • 해당 링크 상태 \(s\)에 대해
         • \(x\)는 변환없고
         • \(x=1\)이라면 \(m\) 증가 유발
  • 가상 링크에 대한 재설정(reset)
    • 두 기본 링크에 대하여 얽힘 교환을 통해 하나의 가상 링크 생성
  • 행동 공간 크기 \(2^3 = 8\)
• 보상(reward):
  • 얽힘 교환이 성공하면 보상 값은 1
  • 그렇지 않으면 보상 값은 0

3. 양자 환경 모델에 대한 가정

• 얽힘 생성 및 저장 방식
  • 얽힘은 신호(herald) 방식으로 생성됨
    • 얽힘 상태가 성공적으로 생성되었을 때, 해당 성공 여부를 외부에서 확인할 수 있도록 신호(herald)를 제공하는 얽힘 생성 기술을 지칭함
    • 양자 얽힘 생성 과정에서 성공 여부를 실시간으로 확인할 수 있음
  • 얽힘 생성 시각과 컷오프 시간 \(t_c\)와의 연관
    • 신호(herald) 방식에 의해 컷오프 시간 \(t_c\)를 정밀하게 측정하여 얽힘 품질 관리에 활용
      • 얽힘 생성 시점부터 시간이 경과함에 따라 얽힘 상태는 열화(decoherence)로 인해 품질이 저하되므로, 컷오프 시간 \(t_c\)이 네트워크 효율 관리에 중요함
  • 얽힘 상태 저장
    • 생성된 얽힘은 양자 메모리에 저장되며, 가상 링크 생성을 위해 얽힘 교환에 사용됨
  • 얽힘 생성 방식으로 DLCZ 기반 프로토콜 사용
    • 광자 방출과 검출을 통해 얽힘 생성 성공 여부를 확인
    • 성공 여부를 기반으로 얽힘 상태를 메모리에 저장하고 컷오프 시간 \(t_c\) 관리
• 시간 슬롯 모델
  • 전체 시간을 슬롯 단위로 나눔
    • 슬롯 길이: \(\frac{L_0}{v}\)
    • \(L_0\): 기본 링크(광섬유)의 길이
    • \(v\): 광섬유에서 빛의 전파 속도
  • 슬롯 길이는 새로운 상태를 관찰하고 링크 생성을 재시도하는데 요구되는 시간보다는 길어야 함
• 기본 링크 얽힘 성공 확률 \(P_{e_{i,j}}\)
  • 광섬유 거리 \(L_0\)에 따라 지수적으로 감소
    • (Sangouard et al., 2009), (missing reference) 또는 (Uphoff et al., 2016)에 제시된 결과에 기반함

Entanglement Generation Probability Model

Once a heralded local entanglement is generated at each node, the two photons must be sent to the BSM and must be measured The entanglement generation probability for an elementary link \(e_{i,j}\) is equal to:

\[P_{e_{i,j}} = \frac{1}{2} \nu^o \left( p e^{-\frac{d_{i,j}}{2L_0}} \right)^2 = \frac{1}{2} \nu^o p^2 e^{-\frac{d_{i,j}}{L_0}}\]

where \(\nu^o\) denotes the optical BSM efficiency (assumed constant at each node, \(\nu^o=0.39\)), \(d_{i,j}\) denotes the length of elementary link \(e_{i,j}\), \(p\) indicates the success probability of detecting a pair of photons during the entanglement generation process (\(p≈0.05\sim0.1\)), \(L_0\)denotes the attenuation length of the optical fiber (\(L_0 = 22 \, \mathrm{km}\)), and the term \(\frac{1}{2}\) accounts for the optical BSM capability of unambiguously identifying only two out of four bell states

• 양자 메모리 효율 \(\eta\)
  • 저장 시간에 따라 감소
    • (Ortu et al., 2022)에서 설명된 Mims 모델에 따름
  • 이는 얽힘 교환 성공 확률 \(P_s\)에 주요 영향을 미침

Quantum Memory Efficiency Model

The efficiency of a quantum memory, denoted as \(\eta(t)\) (the probability that the qubit remains in its original state at time \(t\)), can be expressed as:

\[\eta(t) = \eta(0) \cdot e^{-\frac{t}{T_o}}\]

where \(\eta(0)\) represents the probability that the qubit remains in its original state at time \(t=0\). Typically, \(\eta(0)=1\) for ideal systems but may be less than 1 in practical cases due to initialization imperfections. \(t\) is the time for which the qubit is stored in the quantum memory. \(T_o\) indicates the characteristic memory lifetime or decoherence time, representing the time scale over which the memory retains its original state.

• \(T_o\) (양자 메모리 수명)의 일반적인 값
  • 물리적 시스템별
    • 원자 집합(Atomic Ensembles): 수백 밀리초 ~ 몇 초
    • 이온 트랩(Ion Traps): 진공 상태에서 1초 ~ 100초
    • 고체 상태 양자 메모리(Solid-State Quantum Memory):
      • 희토류 이온: 1~10밀리초
      • NV 센터: 최대 수백 밀리초
    • 초전도 큐비트(Superconducting Qubits): 10~500마이크로초
  • \(T_o\)에 영향을 미치는 요인
    • 환경 잡음: \(T_o\) 감소
    • 온도: 극저온 조건에서 \(T_o\) 증가
    • 오류 보정: 다이나믹 디커플링(Dynamic Decoupling) 등의 기술로 \(T_o\) 연장 가능
  • 양자 네트워크 설계 목표
    • 실용적인 양자 네트워크에서는 최소 \(T_o\)이 1~10초 이상 필요
• 교환 성공 확률 \(P_s\)
  • 얽힘 교환 과정에서 가장 오래된 메모리의 효율 \(\eta(t)\) 에 따라 결정

\[P_s = \eta(t_{oldest}) = \eta(0) \cdot e^{-\frac{t_{oldest}}{T_o}}\]

4. 강화학습 기반 문제 해결 접근 방법

• 확률 모델의 부재
  • 기본 링크 생성 확률 \(P_{e_{i,j}}\)와 메모리 효율 \(\eta\) (따라서, 얽힘 교환 성공 확률 \(P_s\))에 대한 정확한 모델을 알 수 없음
  • 따라서, 당연히 상태 전이 확률 \(p(s_t, a_t, s_{t+1})\)도 알 수 없음
• 깊은 강화학습(DRL)의 적용
  • 가상 링크 생성률을 극대화하는 정책을 찾기 위해 DRL 적용
  • 이 과정에서 \(\pi\)를 따르는 \(Q\)-value 함수인 \(Q^\pi(s, a)\)를 정의하여 활용
• \(Q\)-value 함수 정의
  • \(Q^\pi(s, a)\): 주어진 상태-행동 쌍 \((s, a)\)에 대해 정책 \(\pi\)를 따랐을 때 할인된 누적 보상 기대값 (expected discounted return)
  • 할인된 누적 보상은 궤적(trajectory)에서 미래 보상의 합으로 정의됨: \(\sum_{k=0}^\infty \gamma^k r_{t+k+1}, \quad \gamma \in [0, 1]\)
  • 에이전트는 \(Q\)-value 함수를 극대화하는 최적 정책 \(\pi^*\)를 탐색
• 정책의 구성
  • 본 문제에서 정책은 가장 적절한 컷오프 시간 \(t_c\)를 결정하는 것
• DQN 알고리즘을 활용한 학습
  • 본 연구에서는 Deep Q-Network(DQN) 알고리즘을 기반으로 가상 링크 생성 문제에 적합하도록 학습 루틴을 구성
  • 학습 루틴은 기존의 DQN 방식을 따르면서도 본 연구 문제에 맞게 조정됨

Experimental Results

1. 실험 세팅

• 기본 설정
  • 광섬유 길이 \(L_0 = 100 \, \mathrm{km}\), 빛의 속도(light speed) \(200,000 \, \mathrm{km/s}\)
    • 타임 슬롯 길이 (duration of a time step): \(0.5 \, \mathrm{ms}\)
  • 광섬유 손실은 \(0.2 \, \mathrm{dB/km}\)
    • 광섬유를 통해 빛이 \(1 \, \mathrm{km}\)를 갈 때, 빛의 세기가 조금 줄어드는 정도를 $0.2$로 가정
    • 이 줄어드는 정도는 빛 파장이 \(1,550 \, \mathrm{nm}\) 때 가능
  • Mims 방정식을 사용하여 손실 모델링 수행
  • zero-time efficiency 가정
    • 얽힘 생성, 전송, 또는 교환 과정에서 추가적인 시간 지연(예: 신호 전파 시간, 연산 시간 등)이 없다고 가정
    • 양자 메모리에서 Swap을 수행할 때, 시간이 소모되지 않고 즉각적으로 이루어진다고 간주
• 세 계의 계층으로 이루어진 \(Q\)-value 함수 구현
  • 두 개의 Dense Layer에는 각각 32개의 뉴런 존재
  • 각 층은 \(\tanh\) 활성화 함수를 사용
  • 출력층에는 활성화 함수가 없으며, 액션 수와 동일한 뉴런 수를 가짐
    • 액션 수는 8 (두 개의 기본 링크와 하나의 가상 링크를 고려)
• 학습 알고리즘
  • OpenAI Baselines 라이브러리에서 제공하는 DQN 알고리즘 사용
  • DRL 알고리즘으로 신경망 학습
• 보상 평가
  • 에피소드 보상은 학습 에피소드 동안 발생한 모든 단계의 보상 \(r\)의 합으로 계산
  • 에피소드는 10,000 스텝으로 구성
  • 평균 에피소드 보상이 학습 시간에 따라 증가하며, 600 에피소드 이후 안정화됨

2. 실험 결과

• Benchmark 1: Inf-cutoff-time policy
  • 컷오프 시간 무한대 설정
  • 즉, 첫 번째 기본 링크가 성공적으로 생성되면, 두 번째 기본 링크가 성공할 때까지 첫 번째 링크를 계속 유지
    • 열화(decoherence)로 인해 첫 번째 링크의 상태가 저하되더라도 폐기하지 않고 그대로 사용
  • 이 방법은 최적 정책 성능의 하한선으로 활용됨
  • 장점
    • 첫 번째 링크를 폐기하지 않고 유지하므로, 재생성에 따른 추가 비용과 시간을 절약
  • 단점
    • 첫 번째 링크가 오래 유지되면서 품질이 저하될 가능성이 큼
      • 저하된 품질로 인해 얽힘 교환의 성공 확률이 크게 낮아질 수 있음
• Benchmark 2: Opt-cutoff-time policy
  • 문제의 모든 가능한 컷오프 시간을 시도하여 가장 좋은 결과를 내는 값을 선택
  • 즉, 가장 오래된 기본 링크의 컷오프 시간을 여러 값으로 설정하여 모두 시뮬레이션
    • 각 시뮬레이션 결과를 비교하여 가장 높은 성능(예: 최대 얽힘 교환 성공률)을 내는 컷오프 시간을 선택
  • 이 방법은 최적 정책 성능의 상한선으로 활용됨
• 실험 결과 설명

• 정책 테스트 방법
  • MDP 프로세스를 1,000번 시뮬레이션하여 정책을 테스트
  • 하나의 에피소드는 10,000 스텝으로 구성됨.
• 성능 비교 결과
  • DRL 에이전트는 Inf-cutoff-time 정책보다 명확히 더 좋은 성능을 보임
  • DRL 에이전트의 성능은 opt-cutoff-time 정책에 매우 근접함.
• 컷오프 시간 결과
  • DRL 정책에서 발견된 최적 컷오프 시간: 146.0 스텝
  • opt-cutoff-time 정책에서 발견된 최적 컷오프 시간: 108 스텝
• 의미
  • DRL 정책은 최적 정책(opt-cutoff-time)에 근접하면서도 이 정책에서 사용하고 있는 Brute-force 방법보다 효율적으로 작동함
  • Inf-cutoff-time 정책보다 더 나은 컷오프 시간을 찾음으로써 성능 향상을 입증